Recently created long-term and regionally dispersed satellite-based rainfall estimates have emerged as crucial sources of rainfall data to assess rainfall's spatial and temporal variability, particularly for data-scarce locations. Objective (the general): The purpose of this paper is to assess the skills of nine selected satellite rainfall estimates i.e., (ARC 2.0, TRMM 3B42, CHIRPS v. 2.0, TAMSAT 3.1, CMORPH v. 1.0 adj., PERSIANN CDR and DNRT, and MSWEP v. 2.2) and understand Spatio-temporal variability of rainfall over the Omo River basin using the best performing product. Method: The validation analysis was done by using a point-to-grid-based comparison test at different temporal accumulations. MSWEP was selected as the best product to analyze the long-term trend and variability of rainfall over the Omo-River basin from 1990-2017. The coefficients of variation (CV) and the standardization rainfall anomalies index (SRAI) were used to examine rainfall variability, while the Mann-Kendall (MK) and Sen slope estimators were used to examine the trend and magnitude of rainfall patterns. Results: The overall statistical, categorical, and volumetric validation index results show that the MSWEP is the best performing rainfall product followed by CHRIPS, 3B42, and TAMSAT according to their order of appearance than the remaining products (i.e., ARC, RFE, PER CDR, PER DNRT, and CMORPH). The CV result with the relatively highest monthly variability (CV > 30%) was observed in some southern, northern, southeastern, and central parts of the study area. In general, the overall annual CV shows almost no variation in the entire basin except in the lower part because of the region's prevalent topographic variances, which ranged from 3455 to 352 m.a.s.l. In addition, the highest seasonal positive and negative anomalies are observed in each season in the entire basin. These abnormalities can result in significant floods and droughts that unquestionably influence the basin and its resources. Conclusion: In general, the basin has an increasing trend in the southern portions and a declining trend in the central to northern tip parts of the basin, as can be observed from the annual average MK trend tests. The basin has experienced a greeter variation but is not significant except in some parts of the basin.
| Published in | Hydrology (Volume 12, Issue 2) |
| DOI | 10.11648/j.hyd.20241202.13 |
| Page(s) | 36-51 |
| Creative Commons |
This is an Open Access article, distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution and reproduction in any medium or format, provided the original work is properly cited. |
| Copyright |
Copyright © The Author(s), 2024. Published by Science Publishing Group |
Rainfall, MSWEP, Trends, CHIRPS
Gauge ≥ 1 mm | Gauge < 1 mm | |
|---|---|---|
Satellite ≥ 1 mm | Hit (H) | False alarm (F) |
Satellite < 1 mm | Miss (M) | CD |
Name | ARC | CHRIPS | CMORPH | MSWEP | PE CDR | PER DNRT | RFE | TAMSAT | 3B42 | Perfect. Score |
|---|---|---|---|---|---|---|---|---|---|---|
CORR | 0.242 | 0.246 | 0.316 | 0.311 | 0.286 | 0.286 | 0.255 | 0.339 | 0.318 | 1 |
R2 | 0.06 | 0.06 | 0.10 | 0.10 | 0.08 | 0.08 | 0.07 | 0.11 | 0.10 | 1 |
BIAS | 0.733 | 1.084 | 0.952 | 0.991 | 0.916 | 1.249 | 0.827 | 1.115 | 1.071 | 1 |
PBIAS | -26.7 | 8.391 | -4.778 | -0.862 | -8.367 | 24.88 | -17.283 | 11.482 | 7.132 | 0 |
ME | -1.0 | 0.322 | -0.183 | -0.033 | -0.322 | 0.956 | -0.664 | 0.441 | 0.279 | 0 |
MAE | 4.354 | 5.229 | 4.429 | 4.477 | 4.414 | 5.205 | 4.353 | 4.618 | 4.76 | 0 |
RMSE | 9.241 | 10.365 | 9.137 | 8.99 | 8.398 | 10.194 | 9.053 | 8.674 | 9.518 | 0 |
NSE | -0.32 | -0.659 | -0.275 | -0.254 | -0.086 | -0.603 | -0.264 | -0.16 | -0.38 | 1 |
POD | 0.468 | 0.448 | 0.69 | 0.712 | 0.772 | 0.84 | 0.692 | 0.705 | 0.7 | 1 |
POFD | 0.153 | 0.165 | 0.25 | 0.28 | 0.361 | 0.415 | 0.286 | 0.269 | 0.279 | 0 |
FAR | 0.378 | 0.407 | 0.404 | 0.423 | 0.464 | 0.478 | 0.433 | 0.414 | 0.418 | 0 |
CSI | 0.364 | 0.343 | 0.47 | 0.468 | 0.463 | 0.475 | 0.453 | 0.471 | 0.466 | 1 |
HSS | 0.334 | 0.299 | 0.425 | 0.41 | 0.373 | 0.372 | 0.387 | 0.416 | 0.403 | 1 |
Name | ARC | CHRIPS | CMORPH | MSWEP | PE CDR | PER DNRT | RFE | TAMSAT | 3B42 | Perfect. Score |
|---|---|---|---|---|---|---|---|---|---|---|
CORR | 0.6 | 0.8 | 0.7 | 0.8 | 0.7 | 0.7 | 0.7 | 0.8 | 0.8 | 1 |
R2 | 0.4 | 0.6 | 0.5 | 0.6 | 0.5 | 0.5 | 0.4 | 0.6 | 0.6 | 1 |
BIAS | 0.7 | 1.1 | 1.0 | 1.0 | 0.9 | 1.3 | 0.8 | 1.1 | 1.1 | 1 |
PBIAS | -27.1 | 8.7 | -4.1 | -1 | -8 | 25.1 | -17 | 11.7 | 7.2 | 0 |
ME | -32.1 | 10 | -4.7 | -1.1 | -9.6 | 29.2 | -19.9 | 13.6 | 8.5 | 0 |
MAE | 59.2 | 43.4 | 47.8 | 41.6 | 49.6 | 59 | 53.3 | 50 | 45.6 | 0 |
RMSE | 87.6 | 63.8 | 71.8 | 63.6 | 73.4 | 86.1 | 79.5 | 71.3 | 67.2 | 0 |
NSE | 0.3 | 0.6 | 0.5 | 0.6 | 0.5 | 0.3 | 0.4 | 0.5 | 0.6 | 1 |
POD | 0.9 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 0.9 | 1.0 | 1 |
POFD | 0.3 | 0.9 | 0.4 | 0.6 | 0.9 | 0.8 | 0.7 | 0.4 | 0.7 | 0 |
FAR | 0.0 | 0.1 | 0.0 | 0.0 | 0.1 | 0.1 | 0.0 | 0.0 | 0.0 | 0 |
CSI | 0.9 | 0.9 | 0.9 | 0.9 | 0.9 | 0.9 | 0.9 | 0.9 | 1.0 | 1 |
HSS | 0.5 | 0.1 | 0.6 | 0.5 | 0.2 | 0.3 | 0.4 | 0.4 | 0.4 | 1 |
VHI | 0.7 | 1.0 | 0.9 | 0.9 | 0.9 | 1.0 | 0.8 | 1.0 | 1.0 | 1 |
QPOD | 0.7 | 0.9 | 0.9 | 0.9 | 0.9 | 0.9 | 0.8 | 0.9 | 0.9 | 1 |
VFAR | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.2 | 0.1 | 0.1 | 0.1 | 0 |
QFAR | 0.2 | 0.2 | 0.1 | 0.1 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0 |
VMI | 0.3 | 0.0 | 0.1 | 0.1 | 0.1 | 0.0 | 0.2 | 0.0 | 0.0 | 0 |
QMISS | 0.3 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.2 | 0.1 | 0.1 | 0 |
VCSI | 0.6 | 0.8 | 0.8 | 0.8 | 0.8 | 0.8 | 0.7 | 0.8 | 0.8 | 1 |
QCSI | 0.6 | 0.8 | 0.8 | 0.8 | 0.7 | 0.7 | 0.7 | 0.8 | 0.8 | 1 |
Cat.thres.>= | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | NA |
Vol.thres.value | 80 | 80 | 80 | 80 | 80 | 80 | 80 | 80 | 80 | NA |
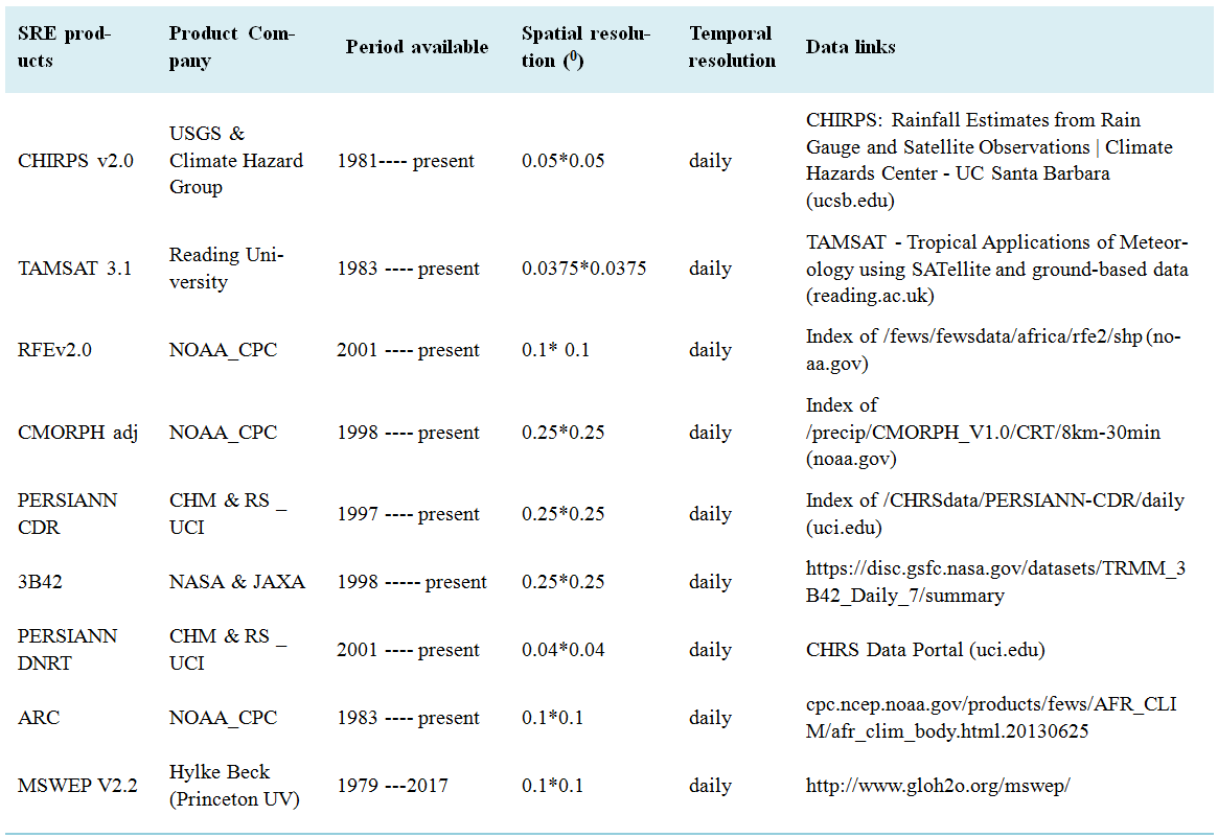
SREPs | Satellite Rainfall Estimation Products |
USAID/(SWP) | U.S. Agency for International Development/ Sustainable Water Partnership |
PMW | Passive Microwave |
TIR | Thermal Infrared |
CCD | Cold Cloud Duration |
ORB | Omo River Basin |
CDT | Climate Data Analysis Tool |
STRM | Shuttle Radar Topography Mission |
TAMSAT | Tropical Applications of Meteorology Using Satellite Data and Ground-Based |
CHIRPS | Climate Hazards Group Infrared Precipitation with Station Data |
MTSAT | Multi-Functional Transport Satellite |
GOES | Geostationary Operational Environmental Satellite Network |
MSWEP | Multi-Source Weighted-Ensemble Precipitation |
| [1] | L. A. Al-Maliki, S. K. Al-Mamoori, I. A. Jasim, K. El-Tawel, N. Al-Ansari, and F. G. Comair, “Perception of climate change effects on water resources: Iraqi undergraduates as a case study,” Arab. J. Geosci., vol. 15, no. 6, p. 503, 2022, |
| [2] | I. Niang et al., “Africa,” Clim. Chang. 2014 Impacts, Adapt. Vulnerability Part B Reg. Asp. Work. Gr. II Contrib. to Fifth Assess. Rep. Intergov. Panel Clim. Chang., pp. 1199–1266, 2015, |
| [3] | USAID/Sustainable Water Partnership (SWP), “Ethiopia Water Resources Profile Overview,” Winrock Int., p. 11, 2021. |
| [4] | M. Li, “Rainfall Distribution in Ethiopia Mengying Li Columbia University,” 2014. |
| [5] | W. Legese, D. Koricha, and K. Ture, “Characteristics of Seasonal Rainfall and its Distribution Over Bale Highland, Southeastern Ethiopia,” J. Earth Sci. Clim. Change, vol. 09, no. 02, 2018, |
| [6] | Z. T. Segele and P. J. Lamb, “Characterization and variability of Kiremt rainy season over Ethiopia,” Meteorol. Atmos. Phys., vol. 89, no. 1, pp. 153–180, 2005, |
| [7] | H. Birara, R. P. Pandey, and S. K. Mishra, “Trend and variability analysis of rainfall and temperature in the tana basin region, Ethiopia,” J. Water Clim. Chang., vol. 9, no. 3, pp. 555–569, 2018, |
| [8] | T. Dinku, P. Ceccato, E. Grover-Kopec, M. Lemma, S. J. Connor, and C. F. Ropelewski, “Validation of satellite rainfall products over East Africa’s complex topography,” Int. J. Remote Sens., vol. 28, no. 7, pp. 1503–1526, 2007, |
| [9] | S. Xiao, J. Xia, and L. Zou, “Evaluation of multi-satellite precipitation products and their ability in capturing the characteristics of extreme climate events over the Yangtze River Basin, China,” Water (Switzerland), vol. 12, no. 4, 2020, |
| [10] | M. M. Alemu and G. T. Bawoke, “Analysis of spatial variability and temporal trends of rainfall in Amhara Region, Ethiopia,” J. Water Clim. Chang., vol. 11, no. 4, pp. 1505–1520, 2020, |
| [11] | N. S. Sinta, A. K. Mohammed, Z. Ahmed, and R. Dambul, “Evaluation of Satellite Precipitation Estimates Over Omo–Gibe River Basin in Ethiopia,” Earth Syst. Environ., vol. 6, no. 1, pp. 263–280, 2022, |
| [12] | T. G. Romilly and M. Gebremichael, “Evaluation of satellite rainfall estimates over Ethiopian river basins,” Hydrol. Earth Syst. Sci., vol. 15, no. 5, pp. 1505–1514, 2011, |
| [13] | G. T. Ayehu, T. Tadesse, B. Gessesse, and T. Dinku, “Validation of new satellite rainfall products over the Upper Blue Nile Basin, Ethiopia,” Atmos. Meas. Tech., vol. 11, no. 4, pp. 1921–1936, 2018, |
| [14] | G. Kabite Wedajo, M. Kebede Muleta, and B. Gessesse Awoke, “Performance evaluation of multiple satellite rainfall products for Dhidhessa River Basin (DRB), Ethiopia,” Atmos. Meas. Tech., vol. 14, no. 3, pp. 2299–2316, 2021, |
| [15] | D. Fenta Mekonnen and M. Disse, “Analyzing the future climate change of Upper Blue Nile River basin using statistical downscaling techniques,” Hydrol. Earth Syst. Sci., vol. 22, no. 4, pp. 2391–2408, 2018. |
| [16] | D. S. Wilks, Statistical methods in the atmospheric sciences, vol. 100. Academic press, 2011. |
| [17] | A. Aghakouchak and A. Mehran, “Extended contingency table: Performance metrics for satellite observations and climate model simulations,” Water Resour. Res., vol. 49, no. 10, pp. 7144–7149, 2013, |
| [18] | H. E. Beck et al., “Daily evaluation of 26 precipitation datasets using Stage-IV gauge-radar data for the CONUS,” Hydrol. Earth Syst. Sci., vol. 23, no. 1, pp. 207–224, 2019, |
| [19] | Y. Kassa, “Addis Ababa Institute of Technology School of Civil and Environmental Engineering Postgraduate Program in Hydraulic Engineering,” no. November, 2013. |
| [20] | M. O. Kisaka, M. Mucheru-Muna, F. K. Ngetich, J. N. Mugwe, D. Mugendi, and F. Mairura, “Rainfall variability, drought characterization, and efficacy of rainfall data reconstruction: Case of Eastern Kenya,” Adv. Meteorol., vol. 2015, 2015, |
| [21] | W. B. Abegaz, “Rainfall Variability and Trends over Central Ethiopia,” Int. J. Environ. Sci. Nat. Resour., vol. 24, no. 4, 2020, |
| [22] | G. Bayable, G. Amare, G. Alemu, and T. Gashaw, “Spatiotemporal variability and trends of rainfall and its association with Pacific Ocean Sea surface temperature in West Harerge Zone, Eastern Ethiopia,” Environ. Syst. Res., vol. 10, no. 1, 2021, |
| [23] | C. Funk et al., “The climate hazards infrared precipitation with stations - A new environmental record for monitoring extremes,” Sci. Data, vol. 2, pp. 1–21, 2015, |
| [24] | J. B. et Al, “Standardized Precipitation Index User Guide,” J. Appl. Bacteriol., vol. 63, no. 3, pp. 197–200, 1987. |
| [25] | S. Ghaedi and A. Shojaian, “Spatial and Temporal Variability of Precipitation Concentration in Iran,” Geogr. Pannonica, vol. 24, no. 4, pp. 244–251, 2020, |
| [26] | F. A. Anose, K. T. Beketie, T. T. Zeleke, D. Y. Ayal, G. L. Feyisa, and B. T. Haile, “Spatiotemporal analysis of droughts characteristics and drivers in the Omo-Gibe River basin, Ethiopia,” Environ. Syst. Res., vol. 11, no. 1, 2022, |
| [27] | P. Nguyen et al., “Persiann dynamic infrared–rain rate (PDIR-now): A near-real-time, quasi-global satellite precipitation dataset,” J. Hydrometeorol., vol. 21, no. 12, pp. 2893–2906, 2020, |
| [28] | K. Teshome and F. Behulu, “Comparison of High-Resolution Satellite Based Rainfall Products at Basin Scale: The Case of Omo-Gibe River Basin, Ethiopia,” vol. 165, no. January, pp. 110–129, 2022. |
| [29] | A. Thesis, “Satellite-Based Rainfall Estimation: Evaluation and Characterization (A Case Study Over Omo-Gibe River Basin),” no. July, 2007. |
| [30] | M. Dembélé and S. J. Zwart, “Evaluation and comparison of satellite-based rainfall products in Burkina Faso, West Africa,” Int. J. Remote Sens., vol. 37, no. 17, pp. 3995–4014, 2016, |
| [31] | T. Dinku, K. Hailemariam, R. Maidment, E. Tarnavsky, and S. Connor, “Combined use of satellite estimates and rain gauge observations to generate high-quality historical rainfall time series over Ethiopia,” Int. J. Climatol., vol. 34, no. 7, pp. 2489–2504, 2014, |
| [32] | M. A. Degefu and W. Bewket, “Variability and trends in rainfall amount and extreme event indices in the Omo-Ghibe River Basin, Ethiopia,” Reg. Environ. Chang., vol. 14, no. 2, pp. 799–810, 2014, |
| [33] | A. Aklilu, A., Alebachew, Assessment of climate change-induced hazards, impacts and responses in the southern lowlands of Ethiopia. Forum for Social Studies, Addis Ababa., no. 4. 2009. |
| [34] | N. Debela, C. Mohammed, K. Bridle, R. Corkrey, and D. McNeil, “Perception of climate change and its impact by smallholders in pastoral/agropastoral systems of Borana, South Ethiopia,” Springerplus, vol. 4, no. 1, 2015, |
| [35] | F. A. Anose, K. T. Beketie, T. Terefe Zeleke, D. Yayeh Ayal, and G. Legese Feyisa, “Spatio-temporal hydro-climate variability in Omo-Gibe River Basin, Ethiopia,” Clim. Serv., vol. 24, p. 100277, 2021, |
| [36] | M. Taye, D. Sahlu, B. F. Zaitchik, and M. Neka, “Evaluation of satellite rainfall estimates for meteorological drought analysis over the upper blue nile basin, Ethiopia,” Geosci., vol. 10, no. 9, pp. 1–22, 2020, |
| [37] | C. J. Carr, River Basin Development and Human Rights in Eastern Africa - A Policy Crossroads. 2017. |
| [38] | M. B. Toma, “Trend Analysis of Climatic and Hydrological Parameters in Ajora-Woybo Watershed, Omo-Gibe River Basin, Ethiopia,” 2021. |
| [39] | A. Asfaw, B. Simane, A. Hassen, and A. Bantider, “Variability and time series trend analysis of rainfall and temperature in northcentral Ethiopia: A case study in Woleka sub-basin,” Weather Clim. Extrem., vol. 19, no. December 2017, pp. 29–41, 2018, |
APA Style
Asefw, E. T., Ayehu, G. T. (2024). Validating the Skills of Satellite Rainfall Products and Spatiotemporal Rainfall Variability Analysis over Omo River Basin in Ethiopia. Hydrology, 12(2), 36-51. https://doi.org/10.11648/j.hyd.20241202.13
ACS Style
Asefw, E. T.; Ayehu, G. T. Validating the Skills of Satellite Rainfall Products and Spatiotemporal Rainfall Variability Analysis over Omo River Basin in Ethiopia. Hydrology. 2024, 12(2), 36-51. doi: 10.11648/j.hyd.20241202.13
AMA Style
Asefw ET, Ayehu GT. Validating the Skills of Satellite Rainfall Products and Spatiotemporal Rainfall Variability Analysis over Omo River Basin in Ethiopia. Hydrology. 2024;12(2):36-51. doi: 10.11648/j.hyd.20241202.13
@article{10.11648/j.hyd.20241202.13,
author = {Elsabet Temesgen Asefw and Getachew Tesfaye Ayehu},
title = {Validating the Skills of Satellite Rainfall Products and Spatiotemporal Rainfall Variability Analysis over Omo River Basin in Ethiopia
},
journal = {Hydrology},
volume = {12},
number = {2},
pages = {36-51},
doi = {10.11648/j.hyd.20241202.13},
url = {https://doi.org/10.11648/j.hyd.20241202.13},
eprint = {https://article.sciencepublishinggroup.com/pdf/10.11648.j.hyd.20241202.13},
abstract = {Recently created long-term and regionally dispersed satellite-based rainfall estimates have emerged as crucial sources of rainfall data to assess rainfall's spatial and temporal variability, particularly for data-scarce locations. Objective (the general): The purpose of this paper is to assess the skills of nine selected satellite rainfall estimates i.e., (ARC 2.0, TRMM 3B42, CHIRPS v. 2.0, TAMSAT 3.1, CMORPH v. 1.0 adj., PERSIANN CDR and DNRT, and MSWEP v. 2.2) and understand Spatio-temporal variability of rainfall over the Omo River basin using the best performing product. Method: The validation analysis was done by using a point-to-grid-based comparison test at different temporal accumulations. MSWEP was selected as the best product to analyze the long-term trend and variability of rainfall over the Omo-River basin from 1990-2017. The coefficients of variation (CV) and the standardization rainfall anomalies index (SRAI) were used to examine rainfall variability, while the Mann-Kendall (MK) and Sen slope estimators were used to examine the trend and magnitude of rainfall patterns. Results: The overall statistical, categorical, and volumetric validation index results show that the MSWEP is the best performing rainfall product followed by CHRIPS, 3B42, and TAMSAT according to their order of appearance than the remaining products (i.e., ARC, RFE, PER CDR, PER DNRT, and CMORPH). The CV result with the relatively highest monthly variability (CV > 30%) was observed in some southern, northern, southeastern, and central parts of the study area. In general, the overall annual CV shows almost no variation in the entire basin except in the lower part because of the region's prevalent topographic variances, which ranged from 3455 to 352 m.a.s.l. In addition, the highest seasonal positive and negative anomalies are observed in each season in the entire basin. These abnormalities can result in significant floods and droughts that unquestionably influence the basin and its resources. Conclusion: In general, the basin has an increasing trend in the southern portions and a declining trend in the central to northern tip parts of the basin, as can be observed from the annual average MK trend tests. The basin has experienced a greeter variation but is not significant except in some parts of the basin.
},
year = {2024}
}
TY - JOUR T1 - Validating the Skills of Satellite Rainfall Products and Spatiotemporal Rainfall Variability Analysis over Omo River Basin in Ethiopia AU - Elsabet Temesgen Asefw AU - Getachew Tesfaye Ayehu Y1 - 2024/06/29 PY - 2024 N1 - https://doi.org/10.11648/j.hyd.20241202.13 DO - 10.11648/j.hyd.20241202.13 T2 - Hydrology JF - Hydrology JO - Hydrology SP - 36 EP - 51 PB - Science Publishing Group SN - 2330-7617 UR - https://doi.org/10.11648/j.hyd.20241202.13 AB - Recently created long-term and regionally dispersed satellite-based rainfall estimates have emerged as crucial sources of rainfall data to assess rainfall's spatial and temporal variability, particularly for data-scarce locations. Objective (the general): The purpose of this paper is to assess the skills of nine selected satellite rainfall estimates i.e., (ARC 2.0, TRMM 3B42, CHIRPS v. 2.0, TAMSAT 3.1, CMORPH v. 1.0 adj., PERSIANN CDR and DNRT, and MSWEP v. 2.2) and understand Spatio-temporal variability of rainfall over the Omo River basin using the best performing product. Method: The validation analysis was done by using a point-to-grid-based comparison test at different temporal accumulations. MSWEP was selected as the best product to analyze the long-term trend and variability of rainfall over the Omo-River basin from 1990-2017. The coefficients of variation (CV) and the standardization rainfall anomalies index (SRAI) were used to examine rainfall variability, while the Mann-Kendall (MK) and Sen slope estimators were used to examine the trend and magnitude of rainfall patterns. Results: The overall statistical, categorical, and volumetric validation index results show that the MSWEP is the best performing rainfall product followed by CHRIPS, 3B42, and TAMSAT according to their order of appearance than the remaining products (i.e., ARC, RFE, PER CDR, PER DNRT, and CMORPH). The CV result with the relatively highest monthly variability (CV > 30%) was observed in some southern, northern, southeastern, and central parts of the study area. In general, the overall annual CV shows almost no variation in the entire basin except in the lower part because of the region's prevalent topographic variances, which ranged from 3455 to 352 m.a.s.l. In addition, the highest seasonal positive and negative anomalies are observed in each season in the entire basin. These abnormalities can result in significant floods and droughts that unquestionably influence the basin and its resources. Conclusion: In general, the basin has an increasing trend in the southern portions and a declining trend in the central to northern tip parts of the basin, as can be observed from the annual average MK trend tests. The basin has experienced a greeter variation but is not significant except in some parts of the basin. VL - 12 IS - 2 ER -